-
Notifications
You must be signed in to change notification settings - Fork 50
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
tangent and curvature #11
Comments
|
Without digging too deep into the numbers, I think this is working as intended. The tangent is the rate of change of the spline -- but it's the rate of change with respect to T, not with respect to X. Your X values increase by 1 for each point, and this library gives one unit of T for each input point, so I would expect the X component of the tangent to always be 1. Eyeballing the graph, it looks like all the points have X=1 The curvature is the rate of change of the tangent, again with respect to T. Because the tangent is 1 at every data point, it is not changing, and its rate of change is 0. And eyeballing the curvature graph, all the points have X=0 |
|
It sounds like you have an independent variable and a dependent variable, and you want to use a spline to relate them? Right now the library is only supporting cases where the independent variable is a fixed interval, but it wouldn't be too hard to add a constructor to the spline type you want to use, which takes T values and their corresponding data points |
|
Yes actually you are completely right. I am in the case you mentioned. Thank you for the answer. |
|
Hello, can you please tell me which of the classes i should modify in order to handle my case of independent variable not at fixed interval? thank you. |
|
You can use Note that the T values will start from 0, instead of from 1 |
|
But if i have point in x y and my x data are not equally distributed and not equally spaced how can i relate those points with t? because then i would like to evaluate the spline as f(x) f'(x) and f''(x) |
|
Ah, I missed that your X values weren't evenly spaced. The is is an interesting problem. There isn't really a mathematically correct way to solve this. One possible idea is having two parallel UniformCubicBSplines - one containing your X values and one containing your Y values.
Then, in order to look up the y value at X=1.25f, create a SplineInverter |
|
Another option is to add a constructor to GenericBSpline: https://github.com/ejmahler/SplineLibrary/blob/master/spline_library/splines/generic_b_spline.h#L189 The existing constructor takes a list of points and auto-computes the knots. The new constructor could take both the points and knots. It could look something like this: GenericBSpline(std::vector<floating_t> knots, const std::vector<InterpolationType> &points, size_t degree)
:SplineImpl<GenericBSplineCommon, InterpolationType,floating_t>(points, points.size() - degree)
{
assert(points.size() > degree);
assert(knots.size() == points.size() + degree - 1);
assert(knots[degree - 1] == 0.0f) // Make this a fuzzy compare, and put "knots[degree - 1] = 0.0f" on the next line?
for(size_t i = 1; i < knots.size(); i++)
{
assert(knots[i] >= knots[i - 1]);
}
this->common = GenericBSplineCommon<InterpolationType, floating_t>(points, std::move(knots), degree);
}Note that you actually need more knots than you do points. Specificially, you need an extra Since we're talking about cubic splines, I would start by setting degree = 3. So you need to insert
Once you do all of this, then you can construct a GenericBSpline with your X values as knots, and your Y values as points: GenericBSpline<float> mySpline(xValues_WithDummyValues, yValues, 3);
float y = mySpline.getPosition(1.5f);If I had to guess, I'd say this approach is goingto be easier than the double-spline suggestion I made above, so start with this. Good luck :) |
|
I am going to try. auto segmentFunction = [this, index](floating_t t) -> floating_t { I tried to use those formula: http://www.qc.edu.hk/math/Certificate%20Level/Parametric%20differentiation.htm but i always get the second derivative scaled of some factor. I dont know the reason. Do you know id those are suitable for the problem? I mean computing the t for a certain x then using the getTangent and the get Curvature and applying those formula? |
|
Maybe i am getting something wrong but i think you cant use as InterpolationType something that is not an array unless changing the templates and also the SplineInverter plus some other utils classes. Am i wrong? |
template<size_t N>
static std::vector<Vector<N>> generateTriangleNumberData(size_t size) {
std::vector<Vector<N>> result(size);
size_t currentTriangleNumber = 0;
for(size_t i = 0; i < size; i++)
{
currentTriangleNumber += i;
Vector<N> nextPosition{};
for(size_t c = 0; c < N; c++) {
nextPosition[c] = currentTriangleNumber;
}
result[i] = nextPosition;
}
return result;
}
void makeSpline(void)
{
float degree = 3;
auto knots = std::vector<float>{-2,-1,0,0.75,1,5,3,4,5,6,7};
auto points = generateTriangleNumberData<1>(knots.size() - (degree - 1));
GenericBSpline<Vector<1>> spline(knots, points, 3);
float interval = 0.5f;
for(size_t i = 0; i < 10; i++) {
auto computedData = spline.getCurvature(i * interval);
}
}
|
|
` void GenericSpline::Fit(const std::vector& X, const std::vector& Y) std::vector knots; data_.push_back(QVector2D(X.at(0), Y.at(0))); From where it come from this auto knots = std::vector{-2,-1,0,0.75,1,5,3,4,5,6,7}; and why do you use a variable interval? Can you please help me? |
|
The problem could be that you're treating your X values as dependent variables. Instead of plotting these values: What happens if you plot these: Think of the input into the spline as your X value (in this case, the variable |
They're just arbitrary numbers I chose for my x values. Let me rename some variablesto make it more similar to your setup and see if that helps: void makeSpline(void)
{
float degree = 3;
std::vector<float> X = std::vector<float>{-2,-1,0,0.75,1,5,3,4,5,6,7};
std::vector<Vector<1>> Y = generateTriangleNumberData<1>(knots.size() - (degree - 1));
GenericBSpline<Vector<1>> spline(X, Y, 3);
float interval = 0.5f;
for(size_t i = 0; i < 10; i++) {
float x = i * interval;
auto computedData = spline.getCurvature(x);
float y = computedData.position[0];
float dy = computedData.tangent[0];
float d2y = computedData.curvature[0];
}
} |
It's just a different way of writing the same thing that you wrote. This: for(float x = 0.0; x < max; x += 0.5) {
//loop code
}is the same as this: float interval = 0.5;
for(int i = 0; i * interval < max; i++) {
float x = i * interval;
//loop code
}But I prefer the second one because there are fewer floating point errors |
|
Thank you. I will try but just a question: |



Hello i am trying to use the library to fit splines on some data. It looks like the derivatives are not working properly.
Maybe i am using the library in the wrong way.
From what i can see the time is not exactly related to the x of each point.
I compute the first derivative at time t : auto d1 = ucbs.getTangent(u).tangent;
I compute the second derivative at time t : auto d2 = ucbs.getCurvature(u).curvature;
then i extract x and y and plot them.
The data are really simple:
(x,y);
(1, 30);
(2, 29);
(3, 27);
(4, 24);
(5, 20);
(6, 16);
(7, 9);
here the curve fitted with an uniform bspline and the two derivatives from the library:
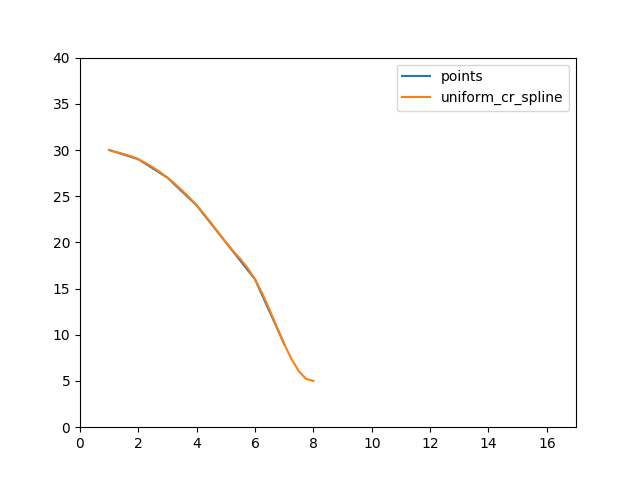
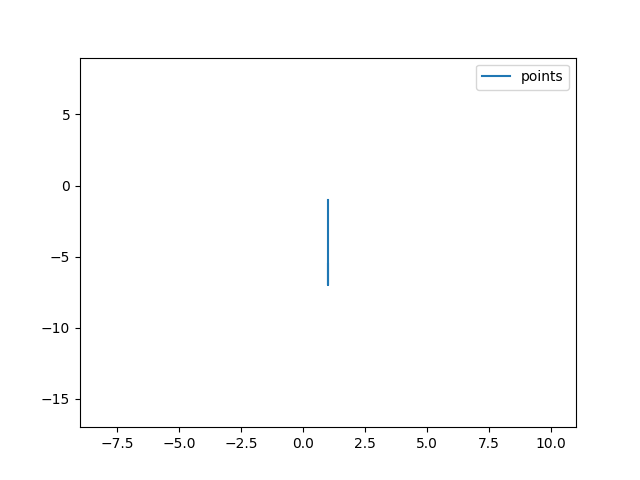
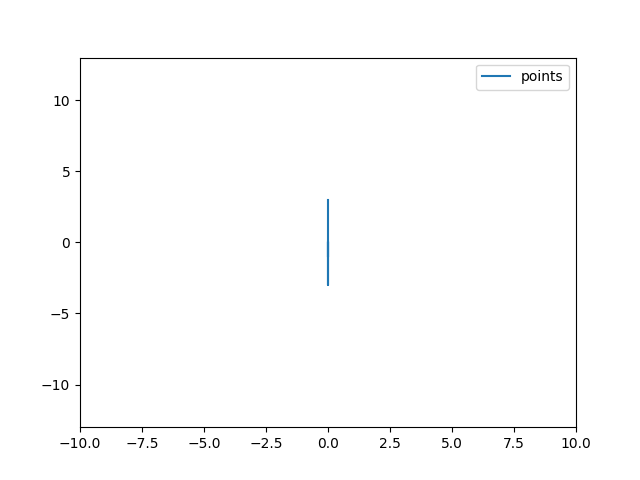
can you help me? Am i using the lib in the wrong way?
The text was updated successfully, but these errors were encountered: