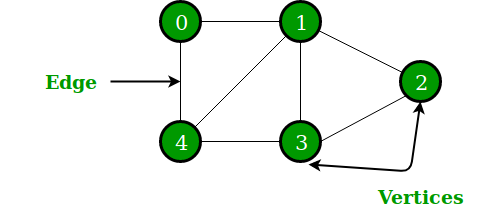
A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph.
A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes.
Here is some common terminology used when working with Graphs:
- Vertex - A vertex, also called a “node”, is a data object that can have zero or more adjacent vertices.
- Edge - An edge is a connection between two nodes.
- Neighbor - The neighbors of a node are its adjacent nodes, i.e., are connected via an edge.
- Degree - The degree of a vertex is the number of edges connected to that vertex.
In the above Graph, the set of vertices V = {0,1,2,3,4} and the set of edges E = {01, 12, 23, 34, 04, 14, 13}.
Graphs are used to solve many real-life problems. Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, Facebook. For example, in Facebook, each person is represented with a vertex(or node). Each node is a structure and contains information like person id, name, gender, locale etc.
Example in real-life
- GPS and Mapping
- Driving Directions
- Social Networks
- Airline Traffic
- Netflix uses graphs for suggestions of products
Undirected Graphs
An Undirected Graph is a graph where each edge is undirected or bi-directional. This means that the undirected graph does not move in any direction.
Directed Graphs (Digraph) Directed Graph also called a Digraph is a graph where every edge is directed.
Unlike an undirected graph, a Digraph has direction. Each node is directed at another node with a specific requirement of what node should be referenced next.
Compare the visual below with the undirected graph above. Can you see the difference? The Digraph has arrows pointing to specific nodes.
Complete Graphs A complete graph is when all nodes are connected to all other nodes.
Connected A connected graph is graph that has all of vertices/nodes have at least one edge.
Disconnected A disconnected graph is a graph where some vertices may not have edges.
An acyclic graph is a directed graph without cycles.
A cycle is when a node can be traversed through and potentially end up back at itself.
We represent graphs through:
Adjacency Matrix
Adjacency List
Email: [email protected]