Aatomic Nature of Matter

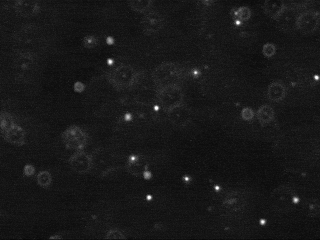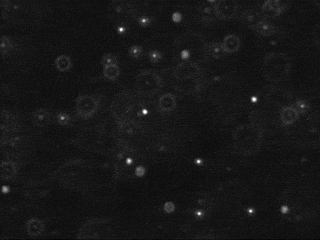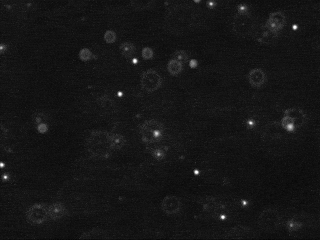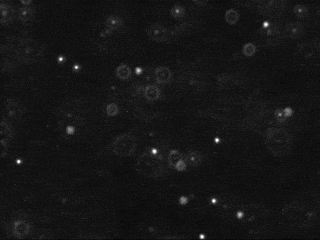
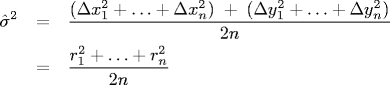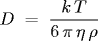Tracking the motion of particles undergoing Brownian motion, fitting this data to Einstein's model, and estimating Avogadro's number

more info

---

A little History

The atom played a central role in 20th century physics and chemistry, but prior to 1908 the reality of atoms and molecules was not universally accepted. In 1827, the botanist Robert Brown observed the random erratic motion of particles found in wildflower pollen grains immersed in water using a microscope. This motion would later become known as Brownian motion. Einstein hypothesized that this Brownian motion was the result of millions of tiny water molecules colliding with the larger pollen grain particles.

In one of his "miraculous year" (1905) papers, Einstein formulated a quantitative theory of Brownian motion in an attempt to justify the "existence of atoms of definite finite size." His theory provided experimentalists with a method to count molecules with an ordinary microscope by observing their collective effect on a larger immersed particle. In 1908 Jean Baptiste Perrin used the recently invented ultramicroscope to experimentally validate Einstein's kinetic theory of Brownian motion, thereby providing the first direct evidence supporting the atomic nature of matter. His experiment also provided one of the earliest estimates of Avogadro's number. For this work, Perrin won the 1926 Nobel Prize in physics.

---

Problem

In this assignment, you will redo a version of Perrin's experiment. Your job is greatly simplified because with modern video and computer technology (in conjunction with your programming skills), it is possible to accurately measure and track the motion of an immersed particle undergoing Brownian motion. We supply video microscopy data of polystyrene spheres ("beads") suspended in water, undergoing Brownian motion. Your task is to write a program to analyze this data, determine how much each bead moves between observations, fit this data to Einstein's model, and estimate Avogadro's number.

---

Solution

1. Particle identification

The first challenge is to identify the beads amidst the noisy data. Each image is 640-by-480 pixels, and each pixel is represented by a Color object which needs to be converted to a luminance value ranging from 0.0 (black) to 255.0 (white). Whiter pixels correspond to beads (foreground) and blacker pixels to water (background). We break the problem into three pieces: (i) read in the picture, (ii) classify the pixels as foreground or background, and (iii) find the disc-shaped clumps of foreground pixels that constitute each bead.

• Read in the image

  You can use opencv, matplotlib, PIL, etc.

• Classify the pixels as foreground or background

  We use a simple, but effective, technique known as thresholding to separate the pixels into foreground and background components: all pixels with monochrome luminance values strictly below some threshold tau are considered background, and all others are considered foreground. The two pictures above illustrates the original frame (above left) and the same frame after thresholding (above right), using tau = 180. This value of tau results in an effective cut for the supplied data.

• Find the blobs

  A polystyrene bead is typically represented by a disc-like shape of at least some minimum number P (typically 25) of connected foreground pixels. A blob or connected component is a maximal set of connected foreground pixels, regardless of its shape or size. We will refer to any blob containing at least P pixels as a bead. The center-of-mass of a blob (or bead) is the average of the x- and y-coordinates of its constituent pixels.

2. Particle tracking

The next step is to determine how far a bead moved from one time step t to the next t + Δt. For our data, Δt = 0.5 seconds per frame. We assume the data is such that each bead moves a relatively small amount, and that two beads do not collide. (However, we must account for the possibility that the bead disappears from the frame, either by departing the microscope's field of view in the x- or y- direction, or moving out of the microscope's depth of focus in the z-direction.) Thus, for each bead at time t + Δt, we calculate the closest bead at time t (in Euclidean distance) and identify these two as the same beads. However, if the distance is too large (greater than delta pixels) we assume that one of the beads has either just begun or ended its journey. We record the displacement that each bead travels in the Δt units of time.

3. Data analysis

Einstein's theory of Brownian motion connects microscopic properties (e.g., radius, diffusivity) of the beads to macroscopic properties (e.g., temperature, viscosity) of the fluid in which the beads are immersed. This amazing theory enables us to estimate Avogadro's number with an ordinary microscope by observing the collective effect of millions of water molecules on the beads.

• Estimating the self-diffusion constant The self-diffusion constant D characterizes the stochastic movement of a molecule (bead) through a homogeneous medium (the water molecules) as a result of random thermal energy. The Einstein-Smoluchowski equation states that the random displacement of a bead in one dimension has a Gaussian distribution with mean zero and variance σ2 = 2 D Δt, where Δt is the time interval between position measurements. That is, a molecule's mean displacement is zero and its mean square displacement is proportional to the elapsed time between measurements, with the constant of proportionality 2D. We estimate σ2 by computing the variance of all observed bead displacements in the x and y directions. Let (Δx1, Δy1), ..., (Δxn, Δyn) be the n bead displacements, and let r1, ..., rn denote the radial displacements. Then

  

  For our data, Δt = 0.5 so this is an estimate for D as well. The radial displacements ri are measured in pixels: to convert to meters, multiply by 0.175 \* 10-6 (meters per pixel).

• Estimating the Boltzmann constant The Stokes-Einstein relation asserts that the self-diffusion constant of a spherical particle immersed in a fluid is given by Stokes-Einstein relation

  

  where, for our data,

    T = absolute temperature = 297 degrees Kelvin (room temperature)
    η = viscosity of water = 9.135 * 10-4 N*s/m2 (at room temperature)
    ρ = radius of bead = 0.5 \* 10-6 meters
  

  and k is the Boltzmann constant. All parameters are given in SI units. The Boltzmann constant is a fundamental physical constant that relates the average kinetic energy of a molecule to its temperature. We estimate k by measuring all of the parameters in the Stokes-Einstein equation, and solving for k.

• Estimating Avogadro's number Avogadro's number NA is defined to be the number of particles in a mole. By definition, k = R / NA, where the universal gas constant R is approximately 8.31457 J K-1 mol-1. Use R / k as an estimate of Avogadro's number.

4. Output formats

Use four digits to the right of the decimal place for all of your floating point outputs whether they are in floating point format or exponential format.

---

Dataset

The dataset that used in this project provided in runs directory.

---

How to use

1. Required Packages

$ pip install numpy pillow

2. Usage

• beadfinder.py

  $ python3 beadfinder.py <min_pixel> <tau> <image>

  • min_pixel (0-INF): minimum pixel of each Blob

  • tau (0-255): the threshold value

  • image: any image in runs/run_/ directory

    e.g:

    $ python3 beadfinder.py 25 180 runs/run_1/frame00001.jpg
    36 ( 49.3889, 477.8611)
    29 ( 82.8276, 214.7241)
    36 (116.6667, 223.6111)
    28 (144.2143, 393.5000)
    35 (214.6000, 310.5143)
    42 (234.8571, 260.2381)
    35 (315.7143, 266.0286)
    31 (355.4516, 286.5806)
    31 (365.4194, 370.9355)
    27 (380.4074, 431.2593)
    37 (399.1351, 299.0541)
    35 (402.1143, 588.5714)
    38 (445.8421, 521.7105)
    

• beadtracker.py

  $ python3 beadtracker.py min_pixel <tau> <delta> <path> > <outputfile>

  • min_pixel (0-INF): minimum pixel of each Blob

  • tau (0-255): the threshold value

  • path: any directory in runs/run_X/* directory

  • outputfile: a file to store the results of displacements

    e.g:

    $ python3 beadtracker.py 25 180 25 runs/run_1/* > displacements_run_01.txt
    

    print output to console:

    $ python3 beadtracker.py 25 180 25 runs/run_1/*
    5.4292
    7.1833
    2.1693
    5.5287
    4.7932
    4.3962
    .
    .
    .
    

• avogadro.py

  $ python3 avogadro.py < <outputfile>

  • outputfile: a file that contains the results of displacements (beadtracker module)

    e.g:

    $ python3 avogadro.py < displacements_run_01.txt
    Boltzmann = 1.2578e-23
    Avogadro = 6.6102e+23
    

    get input directly from beadtracker module:

    $ python3 beadtracker.py 25 180 25 runs/run_1/* | python3 avogadro.py
    Boltzmann = 1.2578e-23
    Avogadro = 6.6102e+23